텍스트 필터링용 trie 구현하기

자료구조 시간에 배우게 되는 자료 구조 중 가장 특이한 애를 꼽자면 해쉬 테이블과 트라이(trie)였다. n-ary tree 처럼 “비교”라는 직관적인 방식을 쓰는게 아니라서 그렇게 느꼈던듯 싶다.

지난 주 후반~오늘까지 텍스트 필터링을 만들면서 이 trie의 일종을 구현하고 테스트했다. 그 와중의 기억을 정리해보는 의미로 여기에 덤프.

필요한 부분이,

• 가능한 범위 내에서 속도가 빠를 것
• 메모리를 적게 쓸 것
• longest-prefix matching; LPM 이 가능할 것
• Unicode (UCS2 or UTF-16LE)를 지원할 것
• 가능하면 MBCS/UTF-8¹를 지원하거나 지원하기 쉬울 것

정도. 덤으로 상황(환경?)은 대충 다음과 같다.

• 전처리 시간은 따로 뺄 수 있다
• 전체 데이터는 메모리에 올릴 수 있는 수준(disk-access 이런거 없음)

그리고 후보였던 자료 구조는 3가진데,

1. (기존에 있던) map/binary-tree 기반의 자료구조
2. trie 기반의 자료구조
3. hash-table 기반의 자료구조

이 중에 기존에 있던 녀석은 메모리 사용량은 그렇다치고(데이터 중복이 많은 편이라 낮지는 않음), 동작 속도의 worst-case가 눈에 띄게 높아서 –_- 일단 보류하고 나머지를 좀 생각했다. hash-table의 경우 imperfect-hashing(=key collison이 있는 경우) 은 trie 보다 느릴 수 있는데, 이번엔 전처리 해도 무방해서 perfect-hashing을 만들어낼 수 있다. 하지만 LPM엔 부적합해서 일단 trie를 쓰기로 했다.

Trie 는 비교를 이용하지 않는다 는 면에서 효율성이 나오는데, 대신 공간은 매우 비효율적으로 쓴다. 노드 자체에 어떤 데이터가 있는지 기록하는 형태가 아니라, 노드 간의 연결이 있고/없음에 데이터의 일부가 기록되는 형태라서, 없는 데이터를 표현하는 공간의 낭비가 심하다. 예를 들어 char 기반의 문자열들을 저장한다고 했을 때, 데이터가 a로 시작하는 단어 100개와 b로 시작하는 단어 100개가 있는 집합이라면, 최상위 노드(root)에서 a, b 항목을 뺀 나머지 공간(적어도 254개 정도)은 쓸모가 없어진다.

속도 문제 때문에 trie를 쓰기로 결정하고 어떻게 하면 메모리를 적게 쓸지 고민하다가 dastrie 란 라이브러리와 이와 관련된 일련의 논문들을 발견했다. 개략적으로 적용할 수 있던 아이디어는,

• trie를 몇 개의 배열을 써서 테이블의 형태로 저장한다²
• 이 때 배열의 갯수는 2개로 한다(원래 3개지만 2개가 같은 인덱스를 쓰기 때문에 하나로 합쳐서 locality를 높인다)
• 다음 링크를 찾을 때 (실제로 현재 노드 밑에서 사용되는 문자의) 최소값/최대값을 이용해서 실제 노드의 수를 줄인다.³
• leaf 부터 시작해서 특정 노드까지 1개의 링크를 따라 배열된 경우, 이를 하나의 문자열로 별도의 배열(tail이라 부름)에 저장한다
• Tail 배열에 대해 중복/suffix인 정보를 써서 추가적인 압축을 시도한다⁴

들이다. 

사실 이거 말고도 (같이 적용할 수 없는 아이디어로) 인덱스 테이블을 cache-coherent 한 해슁으로 처리하는 녀석도 있었다(…). 하지만 키 길이 + 키 갯수를 생각하면 좀 무의미해보여서 기각;

위키백과에서 가져온 이미지에서 이 이야기를 해보자면,

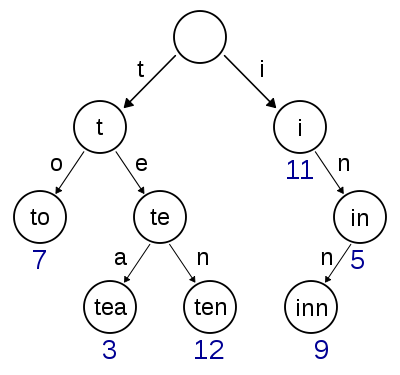
• root 노드는 i ~t 항목까지만 갖는다. (26개의 알파벳 대신 12개의 항목이면된다)
• 2번째 층의 왼쪽 노드역시 e ~ o 항목만 갖는다(11개의 항목).
• root 노드 오른쪽의 경우 inn만이 leaf 노드인데, 그럼 이 녀석을 root 노드 바로 밑의 i 항목에 “inn” 이란 tail로 달아버린다. 노드들이 쭉 제거됨…
• suffix 쪽을 압축할 여지는 없는 트라이다(…)

두 개야 쉽게 생각할 수 있었던 거라 별 문제가 없었지만, 테이블을 쓰는 것 + 최소/최대 인덱스에 관한 것만 저장하기 위한 방법은 꽤나 맘에 드는 것들. base & check 란 두 개의 값을 저장하는 BC란 배열을 두고, i 번째 노드의 정보가 이 배열의 i 번째 항목에 들어가게 한다. 이 정보란건 

• i 번째 노드의 parent 가 몇 번째 항목에 있는지(check)
• i번째 노드의 자식 노드들의 시작 인덱스는 어디인지(base)

다. check가 특정 값(end-marker)면 invalid로 간주하게 하면 좀 당연한 의미고(?), base 값의 활용이 재밌다. char 기반으로 구현되었고 + 현재 노드의 child가 k~m까지 밖에 없다고 하면, 실제 테이블 값은 101번부터~103번까지 저장된다고 하자. 그러면 base 값을 101 – ord('k')⁵ 로 지정한다. 그럼 현재 노드의 child에 대해, 특정 char 값으로 table-lookup을 하면 k~m 사이엔 check 값이 현재 노드로 나오고, 나머지는 그렇지 않게(end-marker나 다른 노드의 값이) 나와서 일종의 trie-압축이 된다. 

이걸 구현하고 나서 처음 닥친 문제점은 비교대상인 원본 프로그램에서 대략 800KiB던 데이터가 37MiB로 불어난 것. 아무래도 wchar_t로 테이블을 만들게 했더니 빈 노드가 너무 늘어난게 원인. 그래서 하나의 wchar_t 문자를 2개의 byte로 쪼개서 저장하게 변경하고 나니 약 1.1MiB 수준으로 감소. 속도는 map을 써서 LPM을 하는 알고리즘의 약 9~10배 정도 빨랐다. 이 정도면 나름대로 만족스러운 성능향상인듯. 

다만 MBCS(DBCS?) or UTF-8 류의 인코딩을 쓰는 것도 처리할 수 있게 변경 하는 문제는 이제 처리해야 한다… 아마 특정 값이 어떤 문자의 마지막 바이트인지 아닌지 확인하는 것만 작성하면 끝날 듯 싶다.